A little Euclidean puzzle
(Audience: Advanced math undergraduates and beyond)
Here's a cute little geometric nonsense that was motivated by a question an undergraduate asked me in Fall 2021, when I was teaching linear algebra. In this post, I will present a little puzzle which I will solve and discuss in the next post.
Consider the set $S$ of (affine) lines in $\mathbb{R}^2$ not passing through the origin. This has a natural topology as follows. (Thanks to Brian in the comments for pointing out the error in Version 1 of this post when discussing these topologies.) For an open set $U \subset \mathbb{R}^2$ and an open set $V \subset S^1$, let $\mathcal{I}(U,V) \subset S$ be the subset of affine lines which intersect $U$ (think that the script $\mathcal{I}$ is for "intersection") and are parallel to an element of $V$.
Exercise: Check that the collection $\{\mathcal{I}(U,V)\}$ is a basis for a topology $\mathcal{T}$ on $S$.
Let $\widetilde{S} = S \cup \{\infty\}$, where we think of $\infty$ as a "line at infinity". To be precise, endow $\widetilde{S}$ with the topology with basis given by subsets of one of the following two forms:
- $\mathcal{I}(U,V)$
- $\{\infty\} \cup (S \setminus \overline{\mathcal{I}(B(r),S^1)})$ where $B(r)$ is the ball of radius $r$ around zero. (The closure is taken within $\mathcal{T}$.)
Exercise: Check that this is a basis for a topology $\widetilde{\mathcal{T}}$ on $\widetilde{S}$ which induces $\mathcal{T}$ on $S$ as the subspace topology.
Define the following two partial operations:
- (Partial) Scalar Multiplication: For $\lambda \in \mathbb{R}^*$ and $\ell \in S$, let $$\lambda \cdot \ell := \left\{\frac{x}{\lambda} \mid x \in \ell \right\}.$$ Notice that this is again an element of $S$.
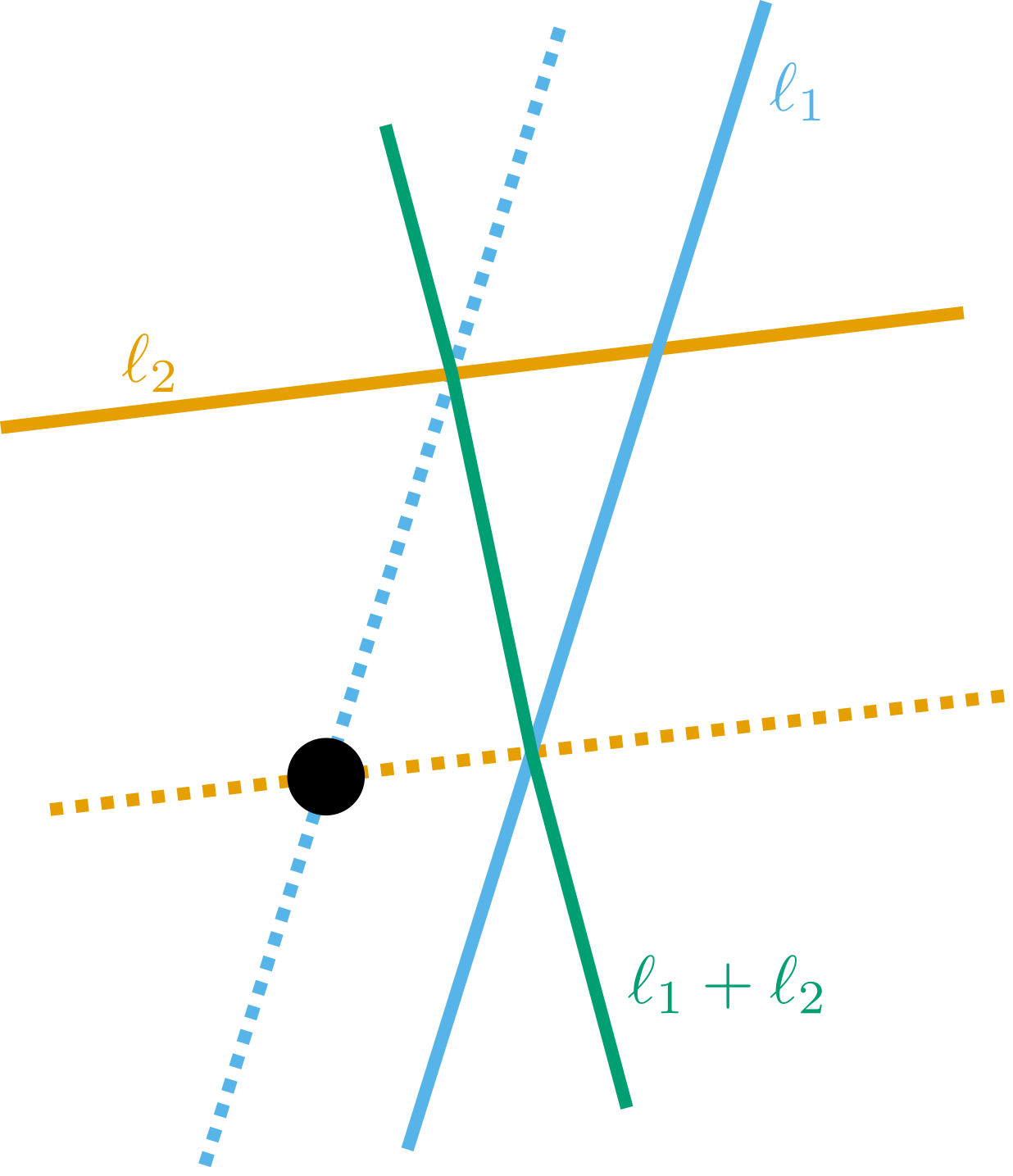
- (Partial) Addition: If $\ell_1,\ell_2 \in S$ (not the line at infinity) are non-parallel, then we perform the following geometric operation. Let $\mu_1$ and $\mu_2$ be the parallel translates of $\ell_1$ and $\ell_2$, but passing through the origin. We obtain a parallelogram bounded by $\ell_1$, $\ell_2$, $\mu_1$, and $\mu_2$. One of the diagonals passes through the origin and the intersection point $\ell_1 \cap \ell_2$. Define $\ell_1 + \ell_2$ by the other diagonal.
Exercise: Prove that these extend uniquely to continuous operations
- Scalar Multiplication: $ \cdot \colon \mathbb{R} \times \widetilde{S} \rightarrow \widetilde{S}$
- Addition: $+ \colon \widetilde{S} \times \widetilde{S} \rightarrow \widetilde{S}$
Hard Exercise / Puzzle: Prove that $\widetilde{S}$ forms a vector space under these operations.
Restatement of Hard Exercise: The hardest part of this puzzle, by far, is associativity, which you can think of as a statement in Euclidean geometry. Suppose we have $\ell_1$, $\ell_2$, and $\ell_3$ three generic lines. You can form this parallelogram type addition to form either $(\ell_1+\ell_2)+\ell_3$ or $\ell_1+(\ell_2+\ell_3)$, and they are incredibly the same!
This feels like it should be a "classical theorem" in Euclidean geometry, but I couldn't find such a statement. I am also unaware of a proof which cannot be rephrased in terms of the overarching solution I will present in the next post. Solutions are welcome in the comments (unless I have already shared this problem with you in person over the last year, in which case I probably already told you the solution).

> Exercise: Check that the collection I(U) gives a topology on S.
ReplyDeleteI don't think this topology is closed under intersection. Take two open disks whose centers lie on a line not through the origin. The intersection of their I(U) is nonempty, but can't contain a line at every angle if they are far enough apart, which any I(U') must.
For a specific example: Let U1 be the open disc of radius 1 centered at (-1000,0.01), and let U2 be the open disc of radius 1 centered at (1000,0.01). Then the intersection of I(U1) and I(U2) is nonempty (it contains the line y=0.01), but it does not contain any lines parallel to the y-axis. Any open set contains a point not on the y-axis, which means that I(U') contains a line parallel to the y-axis for any U'.
ROT13'd spoilers for what I assume your next post is: Gur vairegrq irefvba bs V(H) vf n havba bs yvarf, juvpu vf arire obhaqrq, ohg gurer ner obhaqrq bcra frgf va E^2.
Many thanks for the correction! I indeed intended that nearby lines should be almost parallel, and hence we should include that condition, so I've modified the open sets to be $\mathcal{I}(U,V)$, consisting of lines crossing through an open set $U \subset \mathbb{R}^2$ at angle in an open set $V \subset S^1$. Even with this fix, it's really only a basis for a topology.
DeleteThe inversion v -> v/|v|^2 transforms lines not passing through the origin into circles passing through the origin. Those are entirely determined by their center point. We can rephrase the addition in terms of those circles: take two circles c_1 and c_2 passing through 0, draw the lines l_1 and l_2 passing to 0 and tangent to c_1, resp. c_2, at zero. l_1 intersects c_2 in A and l_2 intersects c_1 in B. Then c_1 + c_2 is the unique circle c_3 passing through A, B and 0. It is a nice Euclidean geometry exercise to show that the center of c_3 is the sum of the centers of c_1 and c_2. Therefore, after applying the inversion, the sum identifies with the usual sum on R^2. Moreover, the scalar multiplication and the topology become the usual ones, hence your space is simply the good old R^2. Is that the solution you had in mind?
ReplyDeleteI give this half credit. You are completely correct, but it's not quite elucidating. I definitely did not come up with the statement by figuring out this "sum of circles" idea and then inverting. Indeed, I think the "sum of circles" is also not such an obvious idea. Also, slightly unsatisfyingly, the sum I define is basis-invariant. You could define it for any two-dimensional vector space $V$ without reference to a basis, whereas inversion requires an inner product. If you use a different inner product, you would be summing ellipses passing through the origin with parallel major and minor axes with the same eccentricity. You can of course apply a linear transformation to get back to circles, but if you can posit a coordinate-invariant version, then you're pretty much at the solution I had in mind, and it should be clear enough that you'll probably be able to guess the question the student in my class had asked me. :)
DeleteOh, I think I see what you mean. It's much less geometric, yet much simpler! :)
Delete